杠杆

杠杆
把一根在力的作用下可绕固定点转动的硬棒叫做杠杆。杠杆可以是任意形状的硬棒。
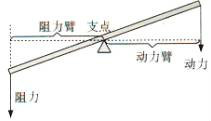
杠杆五要素
(注:动力作用线、阻力作用线、动力臂、阻力臂皆用虚线表示。力臂的下角标随着力的下角标而改变。例:动力为F3,则动力臂为L3;阻力为F5,阻力臂为L5.)

历史
在力的作用下绕固定点转动的硬棒叫做杠杆。
阿基米德在《论平面图形的平衡》一书中最早提出了杠杆原理。他首先把杠杆实际应用中的一些经验知识当作"不证自明的公理",然后从这些公理出发,运用几何学通过严密的逻辑论证,得出了杠杆原理。这些公理是:⑴在无重量的杆的两端离支点相等的距离处挂上相等的重量,它们将平衡;⑵在无重量的杆的两端离支点相等的距离处挂上不相等的重量,重的一端将下倾;⑶在无重量的杆的两端离支点不相等距离处挂上相等重量,距离远的一端将下倾;⑷一个重物的作用可以用几个均匀分布的重物的作用来代替,只要重心的位置保持不变。相反,几个均匀分布的重物可以用一个悬挂在它们的重心处的重物来代替;似图形的重心以相似的方式分布……正是从这些公理出发,在"重心"理论的基础上,阿基米德又发现了杠杆原理,即"二重物平衡时,它们离支点的距离与重量成反比。"
阿基米德对杠杆的研究不仅仅停留在理论方面,而且据此原理还进了一系列的发明创造。据说,他曾经借助杠杆和滑轮组,使停放在沙滩上的桅船顺利下水。在保卫叙拉古免受罗马海军袭击的战斗中,阿基米德利用杠杆原理制造了远、近距离的投石器,利用它射出各种飞弹和巨石攻击敌人,曾把罗马人阻于叙拉古城外达3年之久。
这里还要顺便提及的是,关于杠杆的工作原理,在中国历史上也有记载过。战国时代的墨家曾经总结过这方面的规律,在《墨经》中就有关于天平平衡的记载:“衡木:加重于其一旁,必锤——重相若也。“这句话的意思是:天平衡量的一臂加重物时,另一臂则要加砝码,且两者必须等重,天平才能平衡。这句话对杠杆的平衡说得很全面。里面有等臂的,有不等臂的;有改变两端重量使它偏动的,也有改变两臂长度使它偏动的。这样的记载,在世界物理学史上也是非常有价值的。
平衡条件
相反,几个均匀分布的重物可以用一个悬挂在它们的重心处的重物来代替;似图形的重心以相似的方式分布……正是从这些公理出发,在"重心"理论的基础上,阿基米德又发现了杠杆原理,即"二重物平衡时,它们离支点的距离与重量成反比。
杠杆原理
在使用杠杆时,为了省力,就应该用动力臂比阻力臂长的杠杆;如欲省距离,就应该用动力臂比阻力臂短的杠杆。因此使用杠杆可以省力,也可以省距离。但是,要想省力,就必须多移动距离;要想少移动距离,就必须多费些力。要想又省力而又少移动距离,是不可能实现的。
正是从这些公理出发,在“重心”理论的基础上,阿基米德发现了杠杆原理,即“二重物平衡时,它们离支点的距离与重量成反比。阿基米德对杠杆的研究不仅仅停留在理论方面,而且据此原理还进行了一系列的发明创造。阿基米德曾讲:“给我一个支点和一根足够长的杠杆,我就可以撬动地球”。讲的就是这个道理。但是找不到那么长和坚固的杠杆,也找不到那个立足点和支点。所以撬动地球只是阿基米德的一个假想。
杠杆的支点不一定要在中间,满足下列三个点的系统,基本上就是杠杆:支点、施力点、受力点。其中公式这样写:支点到受力点距离(力矩) * 受力 = 支点到施力点距离(力臂)* 施力,这样就是一个杠杆。杠杆也有省力杠杆跟费力的杠杆,两者皆有但是功能表现不同。例如有一种用脚踩的打气机,或是用手压的榨汁机,就是省力杠杆(力臂 > 力矩);但是我们要压下较大的距离,受力端只有较小的动作。另外有一种费力的杠杆。例如路边的吊车,钓东西的钩子在整个杆的尖端,尾端是支点、中间是油压机 (力矩 > 力臂),这就是费力的杠杆,但费力换来的就是中间的施力点只要动小距离,尖端的挂勾就会移动相当大的距离。两种杠杆都有用处,只是要用的地方要去评估是要省力或是省下动作范围。另外有种东西叫做轮轴,也可以当作是一种杠杆的应用,不过表现尚可能有时要加上转动的计算。
使用杠杆时,如果杠杆静止不动或绕支点匀速转动,那么杠杆就处于平衡状态。
动力臂×动力=阻力臂×阻力,即L1×F1=L2×F2,由此可以演变为F1/F2=L2/L1杠杆的平衡不仅与动力和阻力有关,还与力的作用点及力的作用方向有关。
假如动力臂为阻力臂的n倍,则动力大小为阻力的1/n"大头沉"
动力臂越长越省力,阻力臂越长越费力.
省力杠杆费距离;费力杠杆省距离。
等臂杠杆既不省力,也不费力。可以用它来称量。例如:天平
许多情况下,杠杆是倾斜静止的,这是因为杠杆受到几个平衡力的作用。
详解
杠杆是可以绕着支点旋转的硬棒。当外力作用于杠杆内部任意位置时,杠杆的响应是其操作机制;假若外力的作用点是支点,则杠杆不会出现任何响应。
假设杠杆不会耗散或储存能量,则杠杆的输入功率必等于输出功率。当杠杆绕着支点呈匀角速度旋转运动时,离支点越远,则移动速度越快,离支点越近,则移动速度越慢,由于功率等于作用力乘以速度,离支点越远,则作用力越小,离支点越近,则作用力越大。
分类及应用
一类
支点在动力点和阻力点的中间。称为第一类杠杆。既可能省力的,也可能费力的,主要由支点的位置决定,或者说由臂的长度决定。动力臂与阻力臂长度一致,所以这类杠杆是等臂杠杆。例:跷跷板、天平等。
二类
阻力点在动力点和支点中间。称为第二类杠杆。由于动力臂总是大于阻力臂,所以它是省力杠杆。例:坚果夹子,门,钉书机,跳水板,扳手,开(啤酒)瓶器,(运水泥、砖的)手推车。
三类
动力点在支点和阻力点之间。称为第三类杠杆。特点是动力臂比阻力臂短,所以这类杠杆是费力杠杆,然而能够节省距离。例:镊子,手臂,鱼竿,皮划艇的桨,下颚,锹、扫帚、球棍,理发剪刀等以一手为支点,一手为动力的器械。
变形杠杆
相关内容
文章评论
- 这篇文章还没有收到评论,赶紧来抢沙发吧~
点击排行
- 106-21洗衣机加水前为什么要空转?
- 206-30镜子的发明史
- 306-22牙签简史
- 406-30棉花真的很忙!除了做衣服,它还有这些意想不到的用途
- 502-28火药
- 602-28斜面
- 707-06为什么定向爆破不会影响周围的建筑?
- 807-04石狮子嘴里的小球是怎么放进去的?
- 902-28指南针
- 1002-28四大发明